EDWARD ZAJEC
I turned to the use of computers in 1968. At that time I was experimenting with redundancy in my paintings (repetition of the same module over large areas with only slight shifts in size). The monotony of the manual task and the limited number of variations which I was able to produce in a given time made me realize the inadequacy of traditional methods in dealing with our present reality.
At first I designed programs in which, given a basic repertoire of signs and a set of combinatory rules, the qualitative value of each possible combination depended on a predetermined balance between probability and chance. Later, I tried to extend the autonomy of the programs by developing systems which could produce a number of different combinatory strategies. This was achieved by introducing a determinant tendency which kept referring to a few basic criteria for guidance and qualitative feedback.

When the output of these programs was exhibited as stills in the form of computer graphics, I realized that the structure of the underlying process was of little or no relevance to the viewing public. This opened up a whole set of new problems which could be summed up by saying that no relevant contribution can be made by using the computer in the arts unless the public can be coinvolved as an active participant.
Computer graphics in this context merely represents a transition stage. They stand as stills in a process in motion and fall short of realizing the full potential of the medium. With a computer, we can now describe and communicate the organization, structure, and dynamics of a message. At the same time leaving it open to different interpretations and modifications, or better: only with a computer can we untie the constructive aspects of an idea from its material features and observe and articulate them in time through direct interaction.
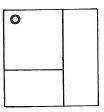
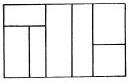
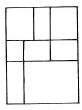
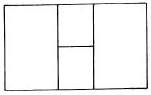
Figure 1
This potential offers the possibility to develop programs which could actively involve the public and turn the passive spectator into an active participant. In designing interactive programs, some attitudes will have to be changed. The artist will no longer concern himself solely with the sublimation and expression of his internal world in the form of finished objects, but will have to deal with specific and locatable problems (even if hypothetical in nature) in order to be able to lend some of the control over to the participant.
I feel that the main shift will therefore have to be from an object oriented art to an art which will emphasize those structural and constructive implications underlying a work or process which are not necessarily stipulated in its formal aspects (or in a final static result) and which can only be communicated in a direct interactive exchange. For example, we can gain very little knowledge about the structural and combinative properties of a system by examining the properties of its constituent elements in isolation. On the contrary, we must actually combine those elements to gain some knowledge about the range of developments which the system may offer. This means that instead of the traditional contemplation, the participant will be offered the possibility to engage in comparison, selection, and decision making; in short, creative participation.
Diagonal White
The procedure described below illustrates the latest version (Diagonal White) of a program which I have been sporadically developing since 1970. At this stage, it is an investigation of the combinatory possibilities of a set of non-determined modules, and of color, simultaneously considered as defining arrangements of differently colored planes, and as the representation of tridimensional space on a plane surface. The constituent elements of the system are: a vertical, a horizontal and a diagonal line for the definition of planes, the three primary colors (yellow, red, blue), and white, gray and black.
The new developments regard the formation of modules (spatial configurations or figures) which are no longer fixed or predetermined, and the color definition of the figure areas in function of their shapes. For this purpose I established an elementary, reciprocal relation between the shape of an area and its chromatic definition, which is exemplified by the following associative rule:
A rectangular area can be either yellow or red or blue.
A non-rectangular area can be either gray or black.
This rule complies with a basic criterion for which the coupling of the primary colors with orthogonal shapes defines flat surfaces in opposition to the coupling of gray and black with non-orthogonal shapes which gives an illusion of tridimensional space. White becomes, in this instance, an ambiguous element for spatial definition as a chromatic counterpart to the diagonal, since it can be considered either as one of the color tones or as the lightest shade in the white/black scale. For this reason it can combine with both orthogonal and non-orthogonal shapes. Therefore except for the definition of the white areas, for the associative rule mentioned earlier, and for certain qualitative tests regarding area size and regularity, the color choice for each area is random in the sense that different color arrangements can define the same composition without altering its spatial definition. The program develops through three separate stages which are functionally related:
Composition.
- Define a rectangle whose sides will be determined by a ratio taken from the Fibonacci series.
- Subdivide the given area into a number of rectangular partitions according to the harmonic proportioning mentioned above.
Notes: The initial rectangle can be subdivided either symmetrically or asymmetrically. The number of partitions is established by a random choice between a minimum and a maximum limit. (Fig. 1)
Figure formation.
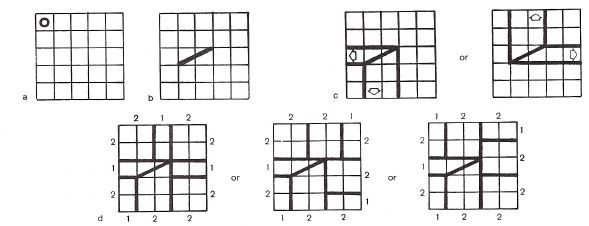
- Insert a matrix in one of the partitions (Fig.2a).
- Position a diagonal element in the given matrix (Fig. 2b).
- Complete the diagonal element by extending a vertical and a horizontal line from each of its two ends (Fig. 2c).
- Subdivide the remaining partition area into rectangles in compliance with the following rhythmic sectioning of the sides: 1,2, 2 or 2,1,2 or 2,2,1 (Fig. 2d).
Notes: The above is only a summary illustration of the figure formation process, since the number of diagonal elements for each figure, and the number of different figures for composition is determined in function of the number of partitions and of the symmetry or asymmetry of the previously established composition.
Color definition.
- Identify the largest non-adjacent rectangular areas, and apply one of the primary colors.
- Apply a second primary color to the remaining non-adjacent rectangular areas.
- Identify all non-adjacent non-rectangular areas and apply either gray or black.
- All the remaining areas are to be white.
Notes: A general rule prevents areas of the same color to have one or more sides in common. When several areas with similar qualifications have common sides, priorities of choice are established by favouring larger size or regularity of shape.
Trieste, Italy
July 1975

Return to Table of Contents | Previous Section | Next Section

