This section will open new vistas in your horizons. We are going to learn how the computer deals with numbers larger than 255, and also how to use the hexadecimal numbering system. Just think of it. Soon you will be a computer brain just like Prototype.

You must always use decimal numbers with a POKE statement. This means that sometimes you will have to convert between binary, hexadecimal and decimal. The "Bits and Bytes" section covered binary numbers where we turn on and off individual bits. In that section you saw that each memory location can only hold numbers up to 255. To store a value larger than that, we just use two locations in a row.

As an example, look at memory locations 88 and 89 which are called SAVMSC. These locations hold a number that tells where the top of the screen is. Because the screen is usually somewhere near the end of memory (it starts at location 40000 in a 48K Atari), at an address that is way beyond the 255 limit for one memory location, the computer needs two locations to store the address. Remember the ranking of the bits where the MSB, or bit seven as we called it, was valued at 128? If we double that rank again, we get 256. Here is the trick to computer math. Since there is no bit eight to give such a rank to, we give the rank to the Entire next byte of 8 bits. Now we just see what the total of this second byte is and multiply it by 256. Figure 1 is a sample:

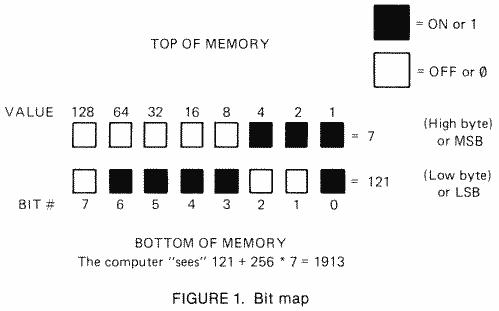
When using two byte numbers, we call the first byte in memory the LOW BYTE because it stores the LOWER VALUE. It can only count from 0 to 255. The second number counts in multiples of 256 and is called the HIGH BYTE.

Let's try to PEEK and POKE a two-byte number. Suppose you wanted to fool the computer into thinking that the screen was in a different place in memory. Such a trick can come in handy when you want to have more than one screen at the same time. First let's look at memory and see where the computer thinks the screen is now. Here's a program to do this:


We know to look in locations 88 and 89 ROM the main part of this book that lists each location in numerical order. This two-byte location is called SAVMSC and points to where the computer thinks the first byte of screen memory is.

When you run the preceding program, the address that gets printed out will vary from 7232 to 40000, depending on how much memory your computer has. What we're going to do is add 480 to this address so that the computer will think that screen memory starts halfway down the current screen. All this means is that no text will print in the top half of the screen, and you'll be able to type below the bottom of the screen (although you won't be able to see anything there).

Let's go ahead and replace the old value of SAVMSC with a new number that is exactly 480 more than the old one. Add the following lines to the preceding ones:


Line 40 finds out what number goes into the high byte of SAVMSC. Remember that the high byte counts the number of pages, or multiples of 256, and that's why we divide by 256.


Now we multiply the new high byte by 256 and subtract it from the total to get the low byte.

Finally we place the new values in memory:


Let's take a look at what the values would be in each step of the program, assuming you have a 16K Atari:


The high byte can count from 0 to 255 just like the low byte. This means the largest number we can have using a two-byte address is:


If we count 0 as a number (since the computer does), that gives a total of 65536, which brings us back again to 64K. We have now come full circle in our discussion, so it is time to go on to something else to challenge you.

---

Return to Table of Contents | Previous Chapter | Next Chapter