The Best of Creative Computing Volume 1 (published 1976)
Turtle Geometry Without Hardware
With these basics of coding for the turtle, the games
played with the real environment eariler can be replayed
with a more abstract representation. It is possible to extend
the basic games in many ways; the following is a list of
variations that can be used to introduce additional
concepts.
We can demonstrate the isomorphism of the movement
of the turtle from one square to another and that of an ant
crawling along a wire as in figure 7.
[image]
Figure 7
The notion of the length of a path can be introduced by
taking as one unit the advance from one square to the next
and thus the length of the path is the number of arcs
followed by the ant above.
The notion of distance between two points can be
introduced through the problem of finding the shortest
path between two squares. One can count these shortest
paths and can find the difference between squares on a grid
for any case given (figure 8).
[image]
Figure 8
The notion of a hamiltonian path can be explored by
finding the longest path without passing through the same
square twice. There is also the question of whether one can
pass through all of the squares by that means.
The notion of transportation time can be studied by
associating an elementary time with each elementary
action. For example, forward may take four seconds,
turning right - 3 seconds, and turning left - 2 seconds.
Thus one can look for the most rapid paths. There can be a
race between two or more turtles subject to the constraint
that they do not simultaneously occupy the same square.
One can add the possibility that the lettuce moves. This
movement can be deterministic (that is to say, known in
advance by the turtle) or random (a game of strategy).
188
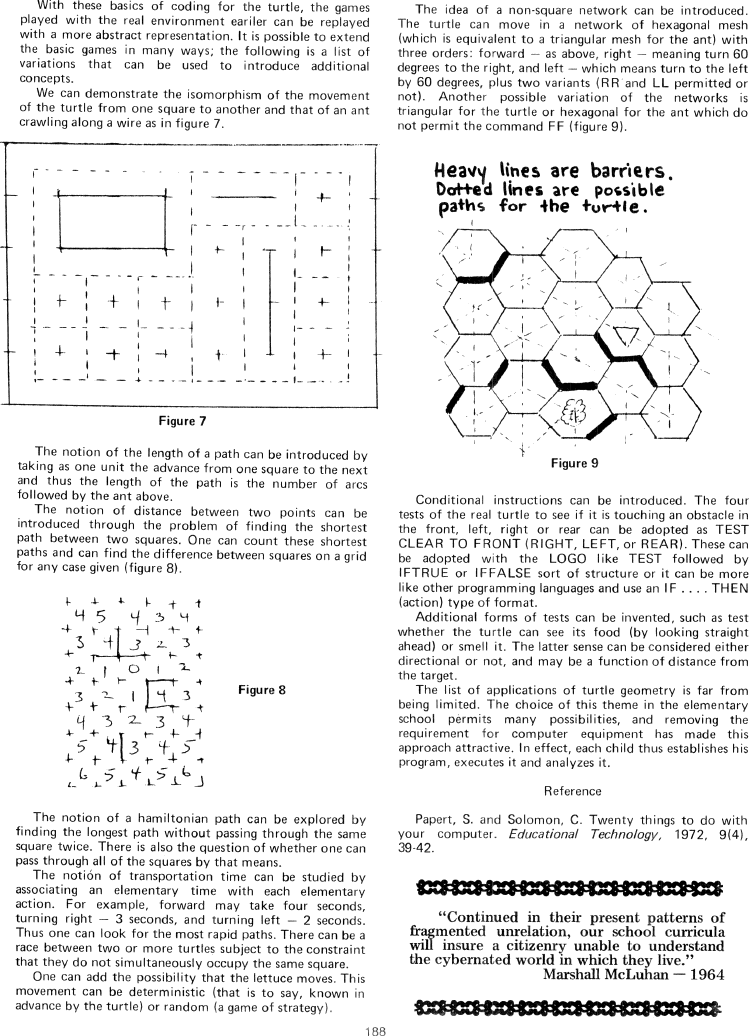
The idea of a non-square network can be introduced.
The turtle can move in a network of hexagonal mesh
(which is equivalent to a triangular mesh for the ant) with
three orders: forward - as above, right - meaning turn 60
degrees to the right, and left - which means turn to the left
by 60 degrees, plus two variants (RR and LL permitted or
not). Another possible variation of the networks is
triangular for the turtle or hexagonal for the ant which do
not permit the command FF (figure 9).
[image]
Conditional instructions can be introduced. The four
tests of the real turtle to see if it is touching an obstacle in
the front, left, right or rear can be adopted as TEST
CLEAR TO FRONT (RIGHT, LEFT, or REAR). These can
be adopted with the LOGO like TEST followed by
IFTRUE or IFFALSE sort of structure or it can be more
like other programming languages and use an IF .... THEN
(action) type of format.
Additional forms of tests can be invented, such as test
whether the turtle can see its food (by looking straight
ahead) or smell it. The latter sense can be considered either
directional or not, and may be a function of distance from
the target.
The list of applications of turtle geometry is far from
being limited. The choice of this theme in the elementary
school permits many possibilities, and removing the
requirement for computer equipment has made this
approach attractive. In effect, each child thus establishes his
program, executes it and analyzes it.
Reference
Papert, S. and Solomon, C. Twenty things to do with
your computer. Educational Technology, 1972, 9(4),
39-42.
[image]
"Continued in their present patterns of
fragmented unrelation, our school curricula
will insure a citizenry unable to understand
the cybernated world in which they live."
Marshall McLuhan - 1964


