SPREADSHEET
PROGRAM WORKS
by Robert Frankston
Robert Frankston is vice-chairman and executive vice-president of Software Arts, Inc., developers of the VisiCalc electronic spreadsheet.
When Dan Bricklin and I wrote the original VisiCalc program in 1979, our goal was to provide a high-performance tool that would allow financial planners the same kind of flexibility enjoyed by people using word processors. The two key ingredients that made this possible were Dan Bricklin's experience with word processing using full-screen editing, coupled with his background in finance, and the availability of low-priced computers.
We had to make many hard decisions in the process of turning our concept into a usable program. Our biggest challenge was creating a package that performed all the necessary sophisticated operations so that the user didn't have to work hard to use it. Some ideas, such as graphics, didn't fit into the Apple computers of that time. On the other hand, we did employ windowing to allow effective use of the screen for viewing more than one part of the spreadsheet. Dan designed much of what VisiCalc should do, and I concentrated on how to make the program do it.
While there are many complicated aspects of implementing the VisiCalc program, the basic idea is quite simple. A spreadsheet program is a computerized version of the traditional accountant's ledger sheet, with added "intelligence" in the form of mathematical or logical relationships between entries or "cells" so that changes in one entry can cause other entries to change accordingly. One of the fundamental mechanisms in any spreadsheet program is the ability to remember the calculation rule for each cell in the sheet. For example, once the user enters a formula, the program is able to remember how to recalculate that cell whenever a value changes.
There are many, many design issues, both technical and aesthetic, associated with writing a spreadsheet program. Rather than give a superficial overview, I will concentrate on specific aspects at the heart of this type of program-the method it uses of keeping track of calculations and performing the calculations each time a value changes. We call this process recalculation since we are calculating again and again and again ... Also, I will describe only the simplest methods for performing an operation.
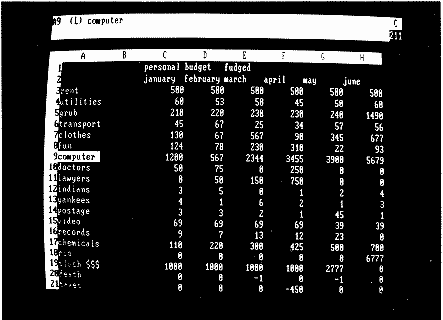
Before we can perform calculations, we must have a representation for the values and the arithmetic expressions. We can think of a spreadsheet as an array of numbers. For example, we can declare the sheet to have 99 rows and 26 columns. Each intersection of rows and columns defines a cell. In addition to a value, each cell on the sheet may have a calculation rule or expression (for budgeting or financial planning) used to compute a new value whenever other values change. Thus the cell B3 (second column, third row) might represent cost and be computed by multiplying the sales in B1 by 80 percent or .8 and adding a fixed cost of $5. We show this as
>B3: +B1*.8+5
The ">" means go to that cell. The ":" is a separator. The "*" means multiply. More technically we say that B3 contains the expression B1 times.8 plus 5. VisiCalc was designed so that we could describe how to set up a spreadsheet in a manual. Thus you can type the example as shown and it will work. Of course, if you are actually using the program, you don't think of B1 or B3; you just think of sales and cost. But if we are trying to understand how the program works inside, then we think of B1 or [2,1] (column 2, row 1) and B3 or [2,3].
The challenge is to allow the user to type in B1*.8+5 so that the value can be recomputed whenever necessary. The least complicated approach is simply to keep the character string that the user typed. VisiCalc itself was originally written in assembly language, although the newer versions are written in a language developed at Software Arts for the purpose of writing and translating programs for different personal computer models. Since I don't want to overwhelm you with technical details, I will describe what the program would do without giving examples of its structure.
When we need to recompute the values (because some value has changed on the spreadsheet), we can look at each column. For each column, we look at the value at each row. When we are done, we have processed all the values on the sheet. When we look at the cell, we must evaluate the expression. This means that if we write 2 + 3*4, we first add 2 and 3 to get 5 and then multiply by 4 to get 20. This is the way it is on most simple calculators.
Computing the value consists of processing the expression from left to right. An expression combines values (or "operands") such as .8 or B1 and operations such as "*" (multiplication) or "+" (addition). If the operand has a cell name (such as B1), we first convert it into a coordinate, [2,1] in this case, then use this to look up the value. We convert B1 by taking the first letter and counting its position in the alphabet. Thus B becomes 2. The row is already a number, so we just use that value.
We then use the "current" value as if the user had typed it instead of the B1. If the current amount is 168, then we are really evaluating "168*.8 + 5." The important thing here is to remember that we are really talking about B1. The next time we evaluate the expression, the value of B1 might be different. Once we have the first value of the expression, we get the following operation ("*") and the following amount. We perform the operation using the value so far (168) and the next one (.8). This 134.4 is now our new value. We then repeat this process until we reach the end of the expression.
The next time we have "+" and "5," so we compute 134.4 + 5 and get 139.4. This is now the value in B3. If we express profit as
B5:B1-B3
we get the first value (168). We then get the operation ("-" for subtraction) and the next value (134.4). The result is 33.6.
If the value in B1 changes to 100, we recalculate and compute 85 for the value in B3. Then, using this result, we compute that the value in B5 is 15.
This is essentially all that is involved in recalculating the values on a spreadsheet. Of course, when we are creating a product, there are many additional considerations. For example:
• Most important is error checking. We must handle these cases gracefully. One method is to use a special value called ERROR as an indication that we can't compute the value. We also extend the numbers to include a "not available" (NA) value.
• The program must run fast. Use of character strings for expressions may be too slow. Instead, we keep the values in a parsed form. This means that we do the analysis of the expression first and store direct references like [2,3] instead of B3. The number can be kept converted into the machine's representation.
• The expressions are richer and more complex. There are many additional functions such as exponentiation, logs and statistical functions. These expressions can have parentheses as well to set them off.
• Coordinate references consist of more than a single letter. Thus AA is equivalent to 27. For some functions (such as SUM) we allow a range instead of a single coordinate. Thus SUM(D1 ... D10) will add the ten numbers in the cells from D1 through D10.
• The user must be able to control the order of evaluation. In the simple example given, if cell A1 refers to cell B1, it won't have the correct value on the first recalculation. There are various approaches to solving this. A list can be kept so that all the expressions dependent on a chained value get recomputed instead of scanning rows and columns.
• In order to handle large sheets in a small amount of memory, we use many space-saving techniques. For example, we don't allocate space for expressions until we need it. Many languages have an ALLOCATE or NEW statement that allows us to do this. We then release it with a FREE or DISPOSE statement.
Input Processing
We have assumed that somehow the expressions have been typed in. Obviously, we need to give the user a means of typing in new expressions and updating old ones. Rather than go into detail here, I will concentrate on how a highly interactive program like VisiCalc differs from using the INPUT statement in BASIC or the READ statement in Pascal. The problem is that if we use the INPUT statement, the user is speaking only to the operating system. What we want instead is to always be available to help the user and give immediate feedback. Thus we completely divorce the input from the output. The user's actions are reflected only in their effect on the spreadsheet.
In the simple case shown, this looks to the user as if we are just typing the character on the screen. Actually, we are making changes to the spreadsheet and showing the effects of the typing. Thus what you see is what you get, and any mistakes you make show up immediately so they can be corrected immediately. This also allows us to guide the user with appropriate prompts.
The most important characteristic of the input is that the program must be readily available in order to give the user the feeling of being in control. Thus, instead of asking for input, the program is always accepting what we enter and will perform an action as soon as it has complete input. When the enter key or an arrow is typed, the expression (or label) is stored at the current position.
The current position is an important concept. It represents the focus for the user activity. Expression entry and many commands apply to this current position. The current position is simply a coordinate such as B3. Whenever we modify the contents of a cell, we must perform the recalculation operation described above. The arrow commands serve to move the coordinate to the next position up, down, left or right.
Redisplay
As with recalculation, we are always recomputing the display. In the simplest view, we just rewrite the screen every time something changes. The challenge is to do this fast enough so it seems instantaneous or to redisplay only the changed portion of the screen.
As we noted in the input processing section, we do not "echo" the user's typing on the screen. Instead we change the sheet-either by changing the contents or by updating a typing buffer, such as one used for the current expression. This effect is shown to the user when the change is made and we redraw the display. Redisplay proceeds by displaying each section of the screen:
Status area. This shows the current position, the contents of the position (i.e., the expression if any) and any additional information such as the recalculation mode.
Prompt. Any prompting information.
Current input. This is used if the user is in the middle of typing an expression or label.
Headers. We display column and row headers.
Cells. We first make sure that the current position is displayable. If it is outside the current window, we must adjust the upper left position to make sure that it is shown. We can then scan the sheet across each row from the upper left position. For each cell, we determine whether it is empty or contains a label or an expression. If there is an expression, we display the current value.
In simplifying my description of the display operation, I have omitted many aspects of VisiCalc such as the optimizations possible, number formating, graphics and other features. In addition, there are many opportunities for new forms of presentation now that high-speed displays are just around the corner.
INTEGRATING SOFTWARE
 Why not? VisiPlot (left) and VisiTrend were the seeds of integrated software. There's nothing revolutionary about the idea for personal computer software that uses the same input for several different applications without swapping disks. On the contrary, "integrated software" is a direct outgrowth of the way business users work at their desktop computers. Once a spreadsheet has been put together, they may want to gain perspective by looking at a chart or comparing their information with the contents of a data base. Or perhaps they'll want to communicate their results by writing a letter or sending electronic mail. Under the standard software philosophy of one program/one disk, implementing these functions is tedious at best-and can be simply impossible if the applications programs use incompatible files. I learned this the hard way when I was designing VisiPlot/ VisiTrend, a graphics package for creating charts from VisiCalc files. To draw up a chart, you had to dump your spreadsheet into a specially formated file, change program disks and then proceed; if you wanted to change a bit of data, you had to return to your VisiCalc model and start all over again. Having a rather eclectic background (including stints as a radio disk jockey and a psychiatric hospital worker), I tended to view things a little differently from my programming colleagues. One day when I was using VisiCalc to project the royalties I'd be making if I ever finished my program, I mentioned to a friend that what VisiCalc needed was a "/G" command that would let us do graphics instantly. He couldn't understand what I was talking about. Then I suggested putting VisiPlot on the same disk with VisiCalc, but this was met with strong objections that VisiCalc would be "polluted." Besides, most personal computers at the time didn't have the necessary internal memory to pull it off. I waited until I was in a position to create a program from the ground up. With the money I got from selling VisiPlot outright, and with assistance from designer John Sachs, I set out to produce a multifunction software package. We hired someone to write a word processing module, but he quit after a month and we settled for a spreadsheet and graphics. We didn't invent "integrated software." Others were also working in this direction, so the term was already in the air. When we saw a program that included a data base, we decided to add this function to our software. We still weren't sure which machine we would release it on, but in August 1982, when IBM introduced its PC with the powerful Intel 8088 processor, we knew this was the computer to go with. That October we announced our program. Originally codenamed Trio, it became known to the world as 1-2-3. When we came up with a more versatile integrated software package complete with word processing and telecommunications ability in 1984, we decided to call it Symphony. It has been suggested that 1-2-3 did for the IBM PC what VisiCalc did for the Apple II, providing a reason for placing these machines on managers' and executives' desks. But the impact just wasn't the same, even though our integrated software has proven extremely popular. We were building on an existing awareness of useful computer functions, not creating an entirely new market. As for the future, we may see the proliferation of a "features race" to cram more and more applications functions onto a single disk. The fact remains that it doesn't matter how many functions you have on a disk; you can only do one thing at a time. It would be nice to receive electronic mail at the same time you're creating a spreadsheet, but this kind of concurrent operation is not practical on today's machines. For the ultimate in integrated software, we'll have to wait for the next generation of personal computers. MITCHELL KAPOR, president of Lotus Development Corporation |
 THE DISCREET Now as ubiquitous as the three-piece suit, whether in its original form or as one of the dozens of sincerely flattering "visiclones" that rival it in sales, VisiCalc is no great shakes to look at. It presents you with a disarmingly simple screen, resembling a vast accountant's ledger made up of 254 rows and 63 columns (though it shows you only a small block of these at any one time). Each box, or "cell," can contain words, numbers, or (and herein lies its genius) formulas that operate on those numbers. In one column, for example, the top cell might contain the label "Expenses." In the cells below there might be a variety of numbers, with the bottom-most cell holding a formula instructing the computer to display the sum of all the numbers in the column. Then, no matter how many numbers are put in the cells on that column, the electronic spreadsheet program gives you a new running total of expenses each time you put it through its paces. But VisiCalc can do far more than just add. Using a simple formula, you can program a cell to add the numbers in the first three rows, subtract the sum from a number held in the next row, multiply the result by a constant, divide by a number from another column, and write the number in a cell somewhere across the sheet. Then, after doing all that, VisiCalc can express the result as a percentage or in scientific notation rounded out to the nearest integer or to twelve decimals. Begin to get the picture? In a trice, VisiCalc makes detailed calculations that would keep a platoon of accountants busy for hours. This is its tour de force, allowing you to get information you wouldn't dare ask for otherwise. It lets you crunch several alternate sets of numbers and compare the results. For the first time, the individual or small business can do what the big-leaguers have always been able to do with large, expensive computers: make several projections based on different assumptions and play them all out on paper. Consider the possibilities. Say you own a widget factory. Here, on a disk, is the ability to reckon the unit cost for each individual widget, taking into account materials, labor, inflation, taxes, shipping and overhead. Should any one of these variables change, you just reenter that one value, press a button and-voila!-the projection's totals are all adapted to the new information. Or, if you're an investor in Consolidated Widget stock and your shares rise ten points while the prime drops a point, a few quick strokes can tell you if it makes sense to refinance the loan you got at 13 percent. The speculative plugging in and recalculating of financial figures have charmingly been called "what-if games." These are the kinds of games that masters of business administration spend two years in B-school playing so they can then creatively improve on a company's balance sheet. Unfortunately, there is a tendency on the part of MBAs and U.S. businessmen in general to rely on such games instead of common sense in running their affairs. It is worth noting that while electronic spreadsheets have been among the most successful personal computer programs in America, their importance overseas has generally been secondary to information filing and retrieval software; in Europe and Japan, it seems, facts are more important than projections. VisiCalc's success on these shores is indicative of America's business culture, including some of its disturbing flaws. Intended as an accurate planning tool, VisiCalc is often used instead to "fudge" financial figures in the eternal search for glowing projections. With some of VisiCalc's results as fictitious as the budget estimates issued by federal agencies and yet just as vital to long-term planning (and waste), it's no wonder that administrators of all stripes have taken to using and abusing its powers. Don't think of it as software; think of it as realpolitik on a disk. DAVID NIMMONS |
| YOUR IRS REFUND CHECK The Internal Revenue Service collects its one hundred million federal income tax returns with ample human help at ten regional centers across the U.S.A. Even so, the growing complexity of the tax code has made it impossible for your refund to be processed quickly without the intervention of computers. After the returns have been sorted, and checks and forms compared and edited by hand for computer processing, tax information is entered on magnetic tape by a clerk at an Automated Collection System terminal. Powerful mainframe computers process the tapes for accuracy with outside data and flag possible audit problems. The National Computer Center for Account Posting and Settlement in Martinsburg, West Virginia, then reconciles all taxpayer tapes, which immediately go to the Treasury Department's Disbursing Center for automated writing of checks. Total elapsed time: three to nine weeks.  |
Return to Table of Contents | Previous Article | Next Article

